The Upper Palaeolithic is commonly defined as the period between c.40,000 BC and 10,000 BC, although neither boundary is particularly well defined. The Upper Palaeolithic is generally split into the Early Upper Palaeolithic and Late Upper Palaeolithic, separated by the Last Glacial Maximum (the peak of the final Pleistocene glaciation). It is now common for a Final/Terminal Upper Palaeolithic to also be distinguished. In many ways the period appears to have seen a similar pattern of activity to that of the preceding Lower–Middle Palaeolithic, with climatic variations apparently resulting in a series of intermittent phases of occupation, the majority of which appear to have been of both limited scale and duration.
The Early Upper Palaeolithic saw the disappearance of the last of the Late Middle Palaeolithic Neanderthal populations and the arrival of fully modern humans, although the exact nature of the interaction (if any) between these two groups remains uncertain. The start of the Early Upper Palaeolithic is largely an archaeological horizon, marking the disappearance of assemblages that characterised Late Middle Palaeolithic activity and the emergence of new technologies and implements.
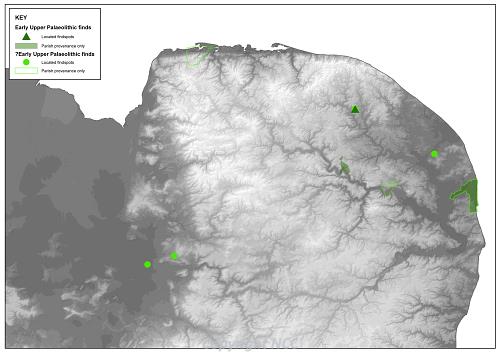
Figure 1. Early Upper Palaeolithic finds.
Two main types of implement appear for the first time at the start of the Early Upper Palaeolithic; bifacial implements known as leaf points and blade leaf points which were made from large retouched blades. The former can be seen as a development of Middle Palaeolithic techniques, whereas the blade leaf points are precursors of the blade-based industries associated with later Upper Palaeolithic phases of activity. Both type of object appear to have been in use around 41,000–40,000 BC and are paralleled by similar material recovered on the continent, and generally assumed to have been produced by Late Neanderthal populations, although the current lack of any associated hominid remains means that this cannot be confirmed at present. A small number of possible leaf points have been found in Norfolk, although most are not recent discoveries and may have been misidentified later prehistoric finds. The most convincing example was found within gravel brought (possibly from Lowestoft) to a building site at Gorleston (NHER 10554; Fig 2).
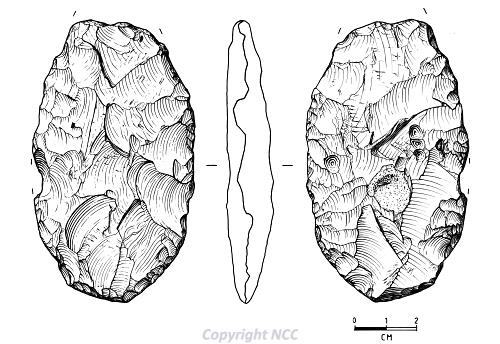
Figure 2. Possible Early Upper Palaeolithic flint leaf point from Gorleston.
Convincing leaf points are similarly scarce, although examples are known from the Drayton/Hellesdon area (NHER 11514) and Colby (NHER 58489; Fig 3). The sparse nature of this evidence is typical for the country as a whole, with very few sites having produced assemblages of any size.
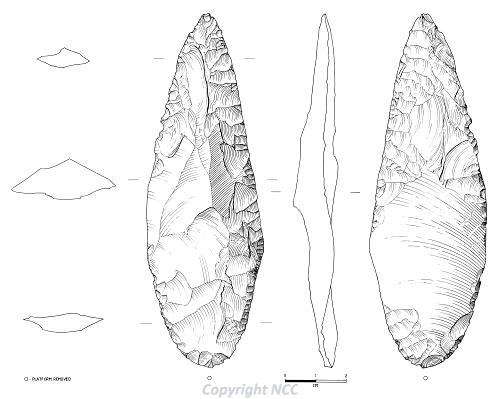
Figure 3. Early Upper Palaeolithic flint blade leaf point from Colby.
The first unambiguous evidence for the presence of fully modern Homo sapiens in north-western Europe are Aurignacian lithic assemblages, although none of the diagnostic implements has so far been identified in Norfolk. The same is true for the subsequent Gravettian dispersal into Britain. Britain was subsequently deserted as conditions deteriorated and was not reoccupied until after the Last Glacial Maximum. Although most of Norfolk lay beyond the southernmost extent of the ice sheet that covered much of Britain at this time arctic peri-glacial conditions would have prevailed until the Late Upper Palaeolithic with the start of a warmer period known as the Late Glacial Windermere Interstadial (c. 12,700–10,800 BC). It is now recognised that the Late Upper Palaeolithic was characterised by a series of different lithic industries, each with its own distinctive diagnostic implements and each quite probably representing a distinct and relatively short-lived phase of dispersal and occupation. Diagnostic implements associated with each of these industries have been identified in several collections recovered from Norfolk, although in all cases the quantities are extremely limited and none are associated with additional material.
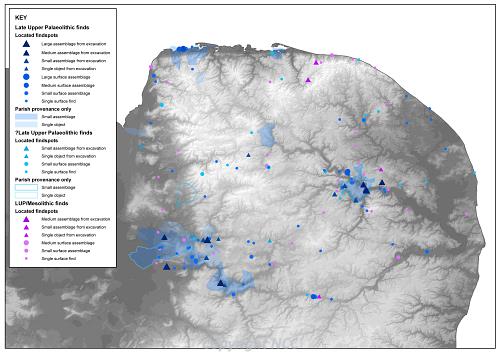
Figure 4. Late Upper Palaeolithic finds.
The first phase of activity during the Late Upper Palaeolithic is known as the Creswellian and is represented in the Norfolk by obliquely truncated backed points (Cresswellian/Cheddar points) from Feltwell (NHER 4895) and Heacham (NHER 1418). A shouldered point of Hamburgian type from Cranwich (NHER 4952) is one of the few objects that can be firmly associated with the following Late Magdalenian phase of activity.
Britain was almost certainly abandoned during the subsequent period of climatic deterioration known as the Older Dryas (c. 12,000 BC) and was not reoccupied until conditions ameliorated during the final phase of the Late Glacial Interstadial (the Allerød). The lithic assemblages associated with this phase of activity are distinguished by the presence of curved-back points (commonly referred to as ‘penknife’ points), examples of which have been found in Norfolk at Weeting (NHER 14951) and Thetford (NHER 5722).
Overall characterising the nature of activity in Norfolk during the Late Upper Palaeolithic is extremely difficult given the dispersed and limited nature of the evidence. There is a hint that the area of the Little Ouse may have been something of a focus for activity at this time, although it should be noted that this is an area that has seen some of the most extensive and intensive surface collection over the last century.
It appears that Britain was again abandoned at the end of the Allerød, prior to the climatic deterioration of the Younger Dryas/Loch Lomond stadial (c. 10,800–9,600 BC) during which there is very little evidence for a human presence in Britain. There is, however, an increasing number of sites which appear to represent activity around the Pleistocene/Holocene transition, that is, between the very end of the Younger Dryas stadial and the start of the Flandrian interglacial (c. 9600 BC). It is these sites that are frequently identified as representing either a Final or Terminal Upper Palaeolithic. The lithic assemblages of this period are characterised by systematically produced long blades, a proportion of which often have distinctive ‘bruised’ edges, possibly resulting from their use as chopping tools. Retouched implements are generally present only in small numbers and take a variety of forms.
A growing number of these long blade assemblages have now been recovered in Norfolk and, given the sparse nature of the evidence for earlier phases of activity, it is reasonable to assume that many of the stray, undiagnostic Upper Palaeolithic finds also relate to Final Upper Palaeolithic activity. Overall the long blade sites appear to show a strong bias towards riverine locations, with relatively few found on the higher ground of the intervening watersheds. The distribution is also markedly uneven, with comparatively dense clusters of sites along the valleys of the River Wissey and Little Ouse in south-west Norfolk and in the valleys of the River Yare and the River Wensum in the vicinity of Norwich. As a result of their frequently low lying situations many of these assemblages have been found to be sealed beneath later fluvial and organic deposits and as a result have survived relatively undisturbed. This was particularly apparent at a site found on the River Wensum at Carrow Road, Norwich, where refitting knapping debris was identified (NHER 26602). Other notable assemblages have also been recovered at Mousehold Heath, Norwich (NHER 51002), Magdalen Street, Norwich (NHER 55569), on the route of the Thetford Bypass (NHER 24849), Hockwold cum Wilton (NHER 5307); Methwold (NHER 4738), Lynford Hall Pit (NHER 21499) and on the foreshore at Titchwell and Thornham (NHER 15352; NHER 1304). In spite of the relatively undisturbed nature of these assemblages little in the way of other associated archaeological evidence has been identified.

Figure 5. Late Upper Palaeolithic flint blade core from Drayton (NHER 20472).
Another feature of this period is the notable variation between assemblages with only some containing a bruised element and markedly different types of other implements. It is unclear at present whether these variations are chronologically significant or whether they represent differences in the primary focus of activity at particular sites. The relationship between these Final Upper Palaeolithic assemblages and the smaller blade assemblages of the Early Mesolithic is also impossible to determine at present, particularly as so few assemblages of either period are associated with precise dating evidence. Although the available scientific dates from across the country suggest a hiatus between the two periods, a number of the implements associated with the Final Upper Palaeolithic are extremely similar to those of associated with Early Mesolithic assemblages.